Problem:
- Given a set of points in a metric space (possibly high dimensional), choose a good set of links between points such that a person could follow links to get progressively closer to some point they have in mind without too much backtracking.
Each point should have a fairly small number of links. Much less than the dimension of the space, which might be high. (This rules out Voronoi diagrams, unfortunately.)
Example applications:
- Explore a space of images. Distance metric might be sum of squared difference between images, or something cleverer.
- Explore a space of documents. Distance metric might be based on word frequencies.
- Augment the set of links in a hyperlinked set of documents. Distance metric would be graph distance.
A first attempt:
- Include a link from A to C if there is no point B such that d(B,A) < d(A,C) and d(B,C) < d(A,C). (That is, a link from A to C may be "occluded" by any point in a lens shaped region between A and C.)
Note that this is defined purely in terms of the distance metric, and is therefore applicable to any metric space (even funny ones like edit distances).
2D Example:
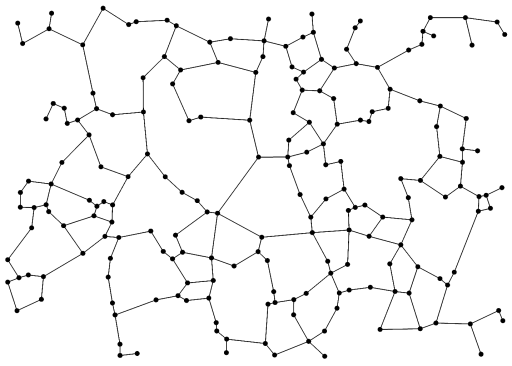
Update 27/7/06: David Eppstein tells me this is called a "Relative Neighborhood Graph". A Relative Neighbourhood Graph is a subset of the Delauny Triangulation, and a superset of the Minimum Spanning Tree. The general problem seems to be known as finding "Proximity Graphs".
Turns out that, as I had hoped, it's been shown that the expected number of edges in a Relative Neighbourhood Graph remains of the same order as the number of nodes even in high dimensions.
Update 28/7/06: This is a page that lets you explore a space of common names, based on an edit distance metric.