Consider a simple mixture model in one dimension, with two classes, the classes having the same spread but different center points. Given that a datum belongs to one of these classes, what is the likelyhood that it belongs to class A?
If Gaussian distributions are used:
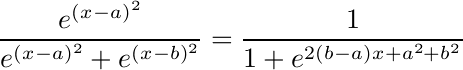
You might recognize this as the logistic function used in neural network models.
If Cauchy distributions are used:
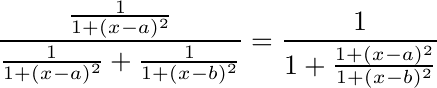
What do these look like?
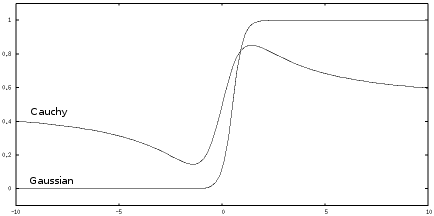
No big surprise if you've been following my previous writing on autism. The autistic Gaussian model says outlier data strongly belongs to the class it is nearer to. The normal Cauchy model says outlier data could belong to either class. This is a useful, common sense thing for the Cauchy model to say. However, it would be hard for a neural network that used the Cauchy curve to implement boolean logic. The Gaussian based curve can be made as close as you like to a sharp binary discrimination, and is much better for implementing boolean logic.
This agrees with the observation that autistic people tend to be overly logical thinkers.