A scale-free distribution used by Chris Wallace, which, gee, Bernie Meyer decided to use at one point as well, a handy-dandy all singing all dancing robustarino distribution:
f(x) = <normalizing constant> * (1+(x/a)^2)^-b
(update: which, as it turns out, is student's t-distribution. ok, so i'm a little slow sometimes... sooo... what we are looking at is a series of independant sample-sets for which we have a conjugate prior consisting of some number of "samples", the more "samples" the more predictable the sample-set... a nice two-parameter model of system governance (number of "samples", sum of squares of "samples") :-) )
I wonder what happens as b goes to infinity.
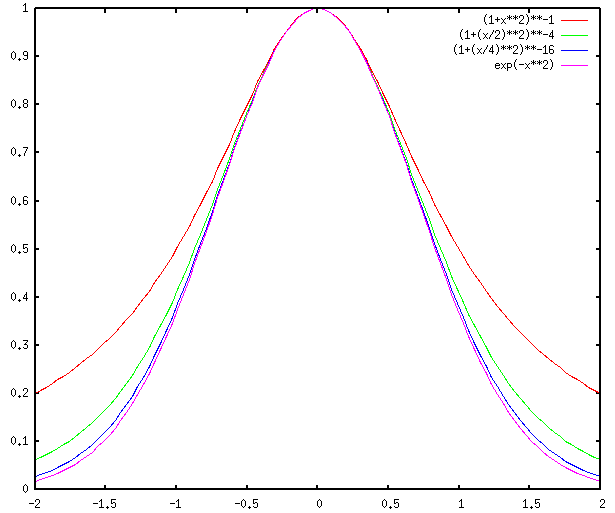
It approaches a Gaussian curve.
Sweet.
Very sweet.
With regards autism, I think this family of distributions is more plausible than the exp(-|x|^p) type distributions. i.e. It's probably not L1 vs L2 so much as b-low vs b-high.